はじめに:タマネギ1.5個は4分の3個!?
先日、家に遊びに来ていた甥っ子(Aくん)とご飯を食べていたときのことです。
Aくんと話していたら食べている料理の材料の話になりました。
その中で妻が、
「この料理に使ったタマネギは 1.5個」
と発言しました。
そしたら、それを聞いたAくんが、
「じゃあ、4分の3 やな」
と言いました。
僕と妻は顔を見合わせてびっくり。
「いやいや、1.5個は4分の3とは違うで。だって、4分の3って1個より少ないやん」
って説明したんですが、Aくんは「えっ???僕、なんかおかしい?」みたいな顔になり、全く分数のルールを理解していないように見えました。
このAくん、学校の成績はいつもいい方だと聞いていたのですが。。
Aくんが「4分の3」と答えた理由
それからしばらく、僕たち夫婦はAくんに分数の数え方を手を変え品を変え説明していました。
そのやりとりの中で、なぜAくんが1.5を4分の3と答えたのか、その理由がようやくわかりました。
実はAくんは頭の中で、2個のタマネギをそれぞれ半分にし、そこから3つ取り出すことで、1.5 => 3/4 を作り出していたのです。

こうやって説明を聞くと、「あー、たしかに4分の3か・・・」と思えなくもありません。
ですが、「タマネギ1.5個 = 3/4個」はやっぱり明らかにおかしいです!
少なくとも「タマネギ2個を1とした場合」という前提条件を付けないと、「タマネギ1.5個 = 3/4」説は成り立ちません。
ティッシュ1/2枚=ティッシュ1/3枚=ティッシュ1枚!?
話はタマネギだけにとどまりません。
本当に分数を理解しているのかどうか確認するために、ティッシュペーパーを渡して「2分の1枚ちょうだい」とお願いしてみました。
僕としてはティッシュを半分にちぎって、片方を渡してくれることを期待したのですが、Aくんは特に迷うこともなく、まるまる1枚のティッシュペーパーを渡してきます。
心の中で「おおっと!?」と思いながら、今度は「じゃあ3分の1枚ちょうだい」とお願いしたら、さっきと同様、まるまる1枚のティッシュペーパーを渡してきます。
なんでっ!?なんでどっちもまるまる1枚渡してくるの!?
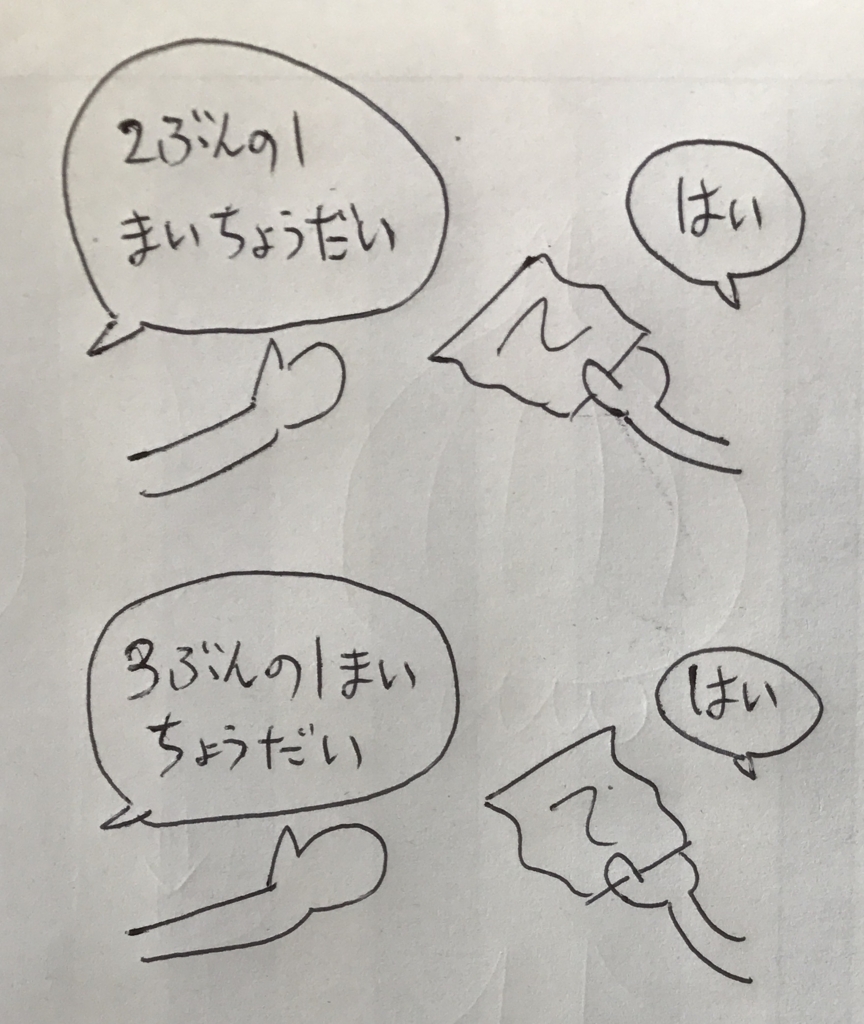
これもどういう理屈でそうなったのか話を聞いてみると、Aくんは、
「ティッシュが3枚あったら、そのうちの1枚で3分の1」
みたいな説明をしてきました。

いやいやいや、そのプラス2枚はいったいどこから出てきたんやっ!?っていう話です 😱
そんなこんなで、最初はいろいろ勘違いしていたAくんですが、あれこれ説明した結果、最終的には正しい答えを返せるようにはなりました。
続き:えっ、みんなそう考えてるの??
「まあ、そんな変わった考え方をするのはAくんぐらいだろうなー」と思いきや、実はそうではありませんでした。
このやりとりをそばで聞いていた娘が、学校に行ってこの話をしたところ、結構な数の同級生の子たちが「3分の1を考えるときは頭の中でティッシュを3枚用意する」と答えたらしいです。
また、妻のママ友の一人も、やはり同じように分数を考えるときは「3つ用意した中の1つ」みたいに考えているらしいです。
もちろん、「3枚あるティッシュのうちの1枚は何分の何?」と聞かれたら「3分の1」でOKです。
でも、「3分の1枚のティッシュ」と言われたら、普通「1枚のティッシュを3等分したうちの1つ」って数えますよね?ね?ね??
(違うのかな?もしかして僕の考え方の方が少数派?)
まとめ:分数と小数の考え方は要再チェック!?
なんでこういう考え方になっちゃうのかなーというのは非常に不思議ですが、子どもに限らず「分数の基準を1以外の都合のいい数字に変えて考える人たち」は意外と多いのかもしれません。
まあ、分数の計算だけにフォーカスするなら、それでも計算はできそうな気がします。
しかし、日常生活で分数や小数を扱うときは基準となる数字を毎回自分の都合のいいように変えてしまうと問題が出てきますよねえ。
というわけで、小学校高学年ぐらいのお子さんがいるお父さんお母さんは、ためしに「1.5個のタマネギって、分数に直したらいくつ?」と聞いてみてください。
もしかすると、びっくりするような答えが返ってくるかもしれませんよ・・・!?